二叉树顺序存储、链式存储及之间转化与遍历。
二叉树的存储可用顺序存储方式和链式存储方式,其中顺序存储时存储地址相邻,空间利用率高,但不易进行元素的增删等操作。而链式存储方式的元素可随意存放,但其存储空间所占为数据元素和指针所占空间,存储空间利用率低。
数据图如下
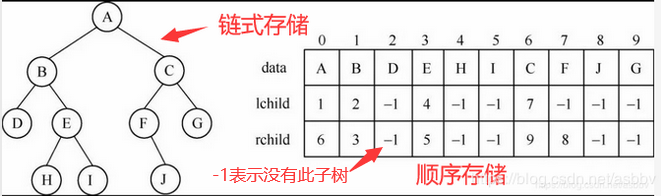
完整程序–转化算法如下
1 |
|
数据图的运行结果
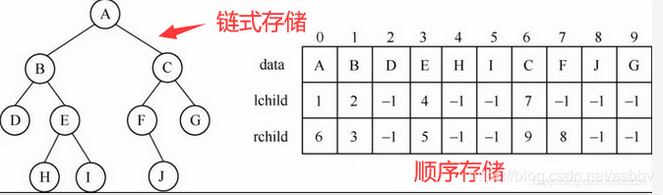

如有问题,欢迎指正。
相关参考资料《数据结构》—周颜军
二叉树的存储可用顺序存储方式和链式存储方式,其中顺序存储时存储地址相邻,空间利用率高,但不易进行元素的增删等操作。而链式存储方式的元素可随意存放,但其存储空间所占为数据元素和指针所占空间,存储空间利用率低。
数据图如下

完整程序–转化算法如下
1 |
|
数据图的运行结果


如有问题,欢迎指正。
相关参考资料《数据结构》—周颜军